Hardy-Weinberg Equilibrium

Hardy-Weinberg Equilibrium#

The Hardy-Weinberg equilibrium (HWE) describes how allele and genotype frequencies remain constant across generations in a population under simple Mendelian inheritance without any interference.

Graphical Summary#

Fig

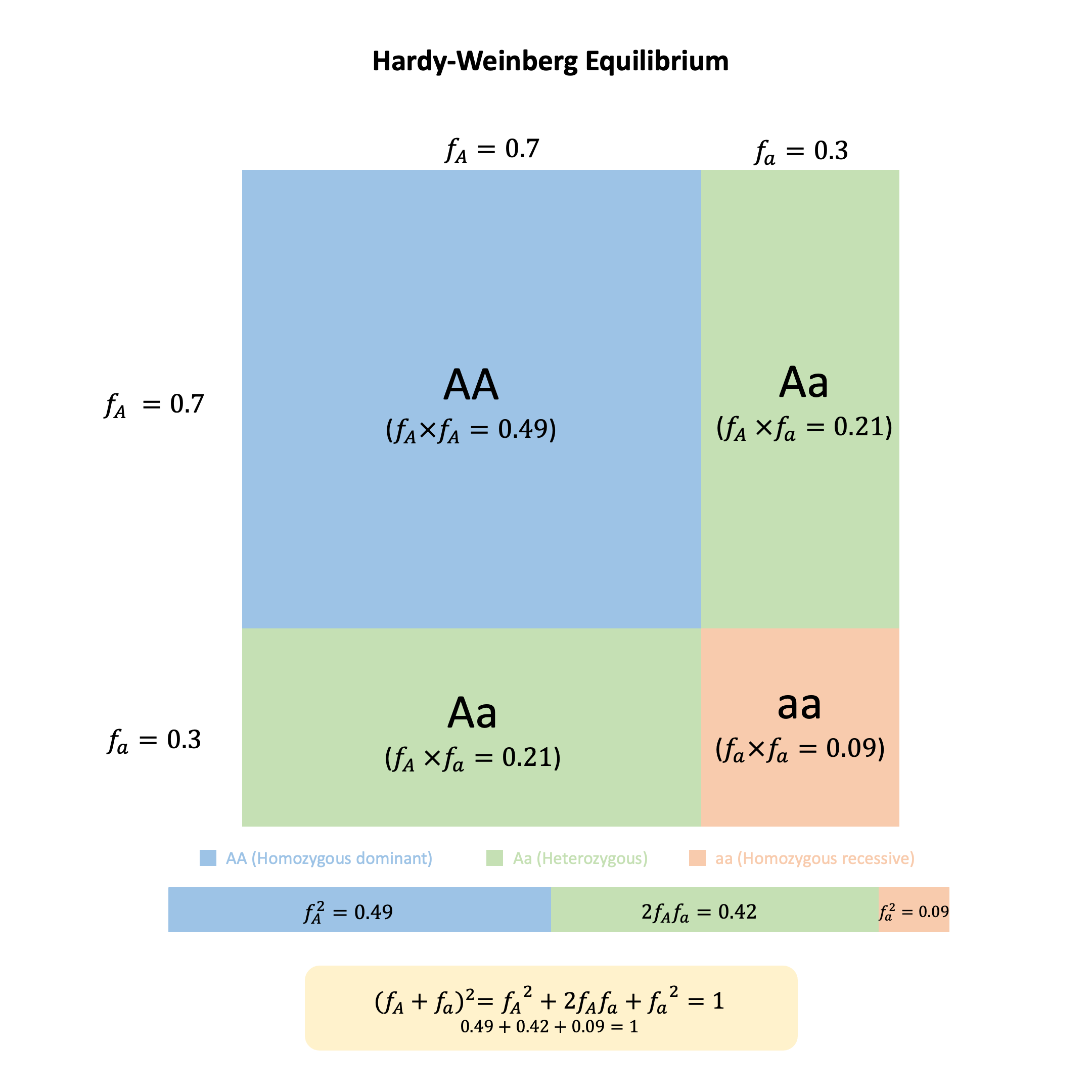
Key Formula#

For a genetic variant with two alleles (A and a) with frequencies \(f_A\) and \(f_a\) respectively (where \(f_A + f_a = 1\)):

\[ (f_A + f_a)^2 = f_A^2 + 2f_A f_a + f_a^2 = 1 \]

Where:

  • \(f_A^2\) = frequency of genotype AA

  • \(2f_A f_a\) = frequency of genotype Aa

  • \(f_a^2\) = frequency of genotype aa

HWE is fundamentally a binomial expansion with power 2. The general intuition of binomial expansion is: if you have two options and you make the choice \(n\) times, what are the possible outcomes and how frequently is each one?

In HWE, we have two alleles (A and a) and we’re making the “choice” twice (once from each parent), so \(n=2\). The binomial expansion \((f_A + f_a)^2\) directly gives us:

  • How many ways to get each genotype combination

  • The probability of each genotype under random mating

This mathematical structure immediately tells us that HWE is about random sampling of alleles twice - exactly what happens when two parents contribute one allele each to their offspring under Mendelian inheritance.

Technical Details#

Setup a Contingency Table#

If HWE holds, it means maternal and paternal alleles are chosen independently (as in our binomial expansion). We can test this independence directly using a 2×2 contingency table.

Set up the data as:

Paternal A

Paternal a

Maternal A

AA count

Aa count

Maternal a

Aa count

aa count

Under HWE, the odds ratio should approximately equal 1.0 (which we will discuss further in Lecture: odds ratio), meaning:

  • The odds of getting allele A vs. a from the father are the same regardless of which allele came from the mother

  • Maternal and paternal allele choices are independent (exactly what our binomial expansion assumes)

When HWE Doesn’t Hold#

Common reasons why we might see deviations from HWE:

  • Non-random mating: People don’t choose partners randomly - they might prefer similar traits, leading to more homozygotes than expected

  • Population mixing: When people from different populations have children together, it can create patterns that don’t match HWE

  • Technical issues: Genotyping errors or poor DNA quality can make it look like HWE is violated

Why HWE Matters in Practice#

  • Quality control: If many genetic variants violate HWE in your dataset, it often means there are technical problems with the genotyping

  • Baseline expectation: HWE tells us what “normal” looks like, so we can spot when something interesting (or problematic) is happening

Example#

We demonstrate how to test for Hardy-Weinberg equilibrium using the classic scarlet tiger moth data in Example 1 in Lecture: odds ratio. This example shows how to set up a 2×2 contingency table to test independence of maternal and paternal alleles, calculate odds ratios, and perform chi-square tests to determine if HWE holds in real data. Now you can skip this section.

Contents