Minor Allele Frequency

Minor Allele Frequency#

The minor allele frequency (MAF) represents the proportion of the less common allele in a population, which equals half the expected genotype value under additive model in diploid organisms like humans since each individual carries two alleles per locus.

Graphical Summary#

Fig

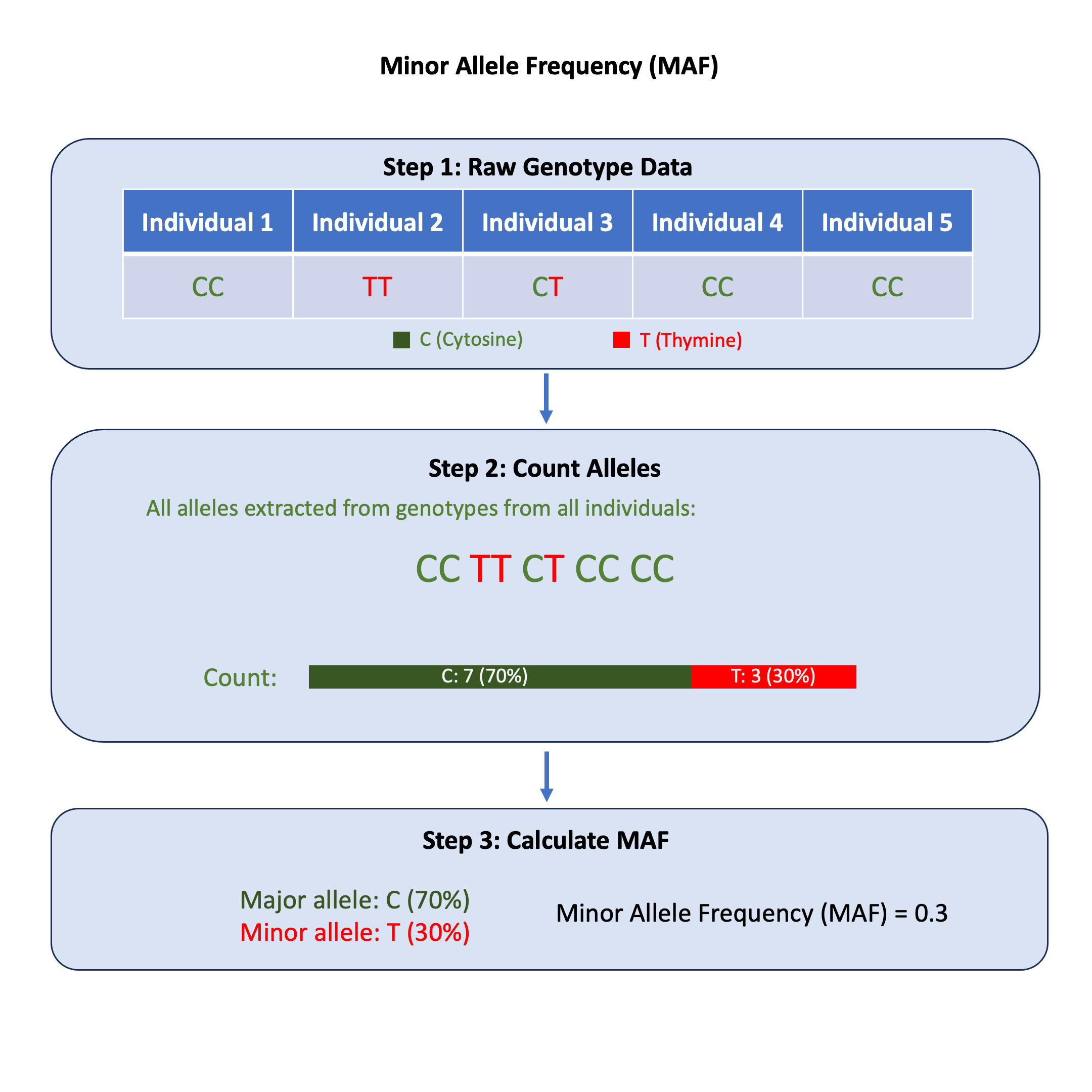
Key Formula#

\[ \text{MAF}_j = \frac{\mathbb{E}[X_{\text{additive},j}]}{2} = \frac{1}{2N}\sum_{i=1}^{N} X_{\text{additive},ij} \]

Where:

  • \(X_{\text{additive},ij}\) represents the count of alternative alleles (0,1,2) for individual \(i\) at the \(j\)-th variant.

  • The division by 2 is necessary because in the additive model for diploid organisms, each individual contributes two alleles.

Technical Details#

If there are only two alleles at the same locus, then the frequency of them can be denoted as \(f_j\) and \(1-f_j\). The \(\text{MAF}_j\) is always defined as:

\[ \min(f_j, 1 - f_j) \]

which ensures that it always represents the frequency of the less common allele in the population, i.e., minor allele.

If there are more alleles, the MAF is specific for each minor allele.

Example#

Using the same genetic data from 5 individuals at 3 variants as we did in Lecture: genotype coding, how do we calculate the minor allele frequency (MAF) for each variant? What’s the simplest way to estimate MAF from our sample data, and how do we implement this method of moments approach in R?

(Note: while this gives us a quick estimate, we’ll see later in the Lecture: maximum likelihood estimation how MAF is typically calculated in practice.)

# Clear the environment
rm(list = ls())

# Define genotypes for 5 individuals at 3 variants
# These represent actual alleles at each position
# For example, Individual 1 has genotypes: CC, CT, AT
genotypes <- c(
 "CC", "CT", "AT",  # Individual 1
 "TT", "TT", "AA",  # Individual 2
 "CT", "CT", "AA",  # Individual 3
 "CC", "TT", "AA",  # Individual 4
 "CC", "CC", "TT"   # Individual 5
)
# Reshape into a matrix
N = 5
M = 3
geno_matrix <- matrix(genotypes, nrow = N, ncol = M, byrow = TRUE)
rownames(geno_matrix) <- paste("Individual", 1:N)
colnames(geno_matrix) <- paste("Variant", 1:M)

The raw genotype matrix is:

geno_matrix
A matrix: 5 x 3 of type chr
Variant 1Variant 2Variant 3
Individual 1CCCTAT
Individual 2TTTTAA
Individual 3CTCTAA
Individual 4CCTTAA
Individual 5CCCCTT
 
# Initialize the output data frame
maf_results <- data.frame(
  Variant = colnames(geno_matrix),
  Major_Allele = character(M),
  Minor_Allele = character(M),
  MAF = numeric(M),
  stringsAsFactors = FALSE
)

For each variant we first the extract the two alleles, then count the frequency of each allele to identify which one is major and which one is minor. At last we calculate the MAF of each variant.

# Process each variant separately
for (j in 1:M) {
  variant_name <- colnames(geno_matrix)[j]  
  # Step 1: Extract all alleles from the genotype column
  alleles <- c()
  for (genotype in geno_matrix[, j]) {
    # Extract first and second allele from each genotype
    first_allele <- substr(genotype, 1, 1)
    second_allele <- substr(genotype, 2, 2)
    alleles <- c(alleles, first_allele, second_allele)
  }
  
  # Count frequency of each allele
  allele_table <- table(alleles)
  total_alleles <- sum(allele_table)
  allele_freq <- allele_table / total_alleles
  
  # Step 2: Identify major and minor alleles
  ordered_freqs <- sort(allele_freq, decreasing = TRUE)
  major_allele <- names(ordered_freqs)[1]
  minor_allele <- names(ordered_freqs)[2]
  
  # Step 3: Calculate minor allele frequency (MAF)
  minor_freq <- ordered_freqs[2]
  maf_results$Major_Allele[j] <- major_allele
  maf_results$Minor_Allele[j] <- minor_allele
  maf_results$MAF[j] <- minor_freq
}

The minor allele frequencies for the three variants are:

maf_results
A data.frame: 3 x 4
VariantMajor_AlleleMinor_AlleleMAF
<chr><chr><chr><dbl>
Variant 1CT0.3
Variant 2TC0.4
Variant 3AT0.3
Contents