Confounder

Confounder#

A confounder is a variable that influences both the exposure and outcome independently, creating a misleading association between them that doesn’t represent a true causal relationship.

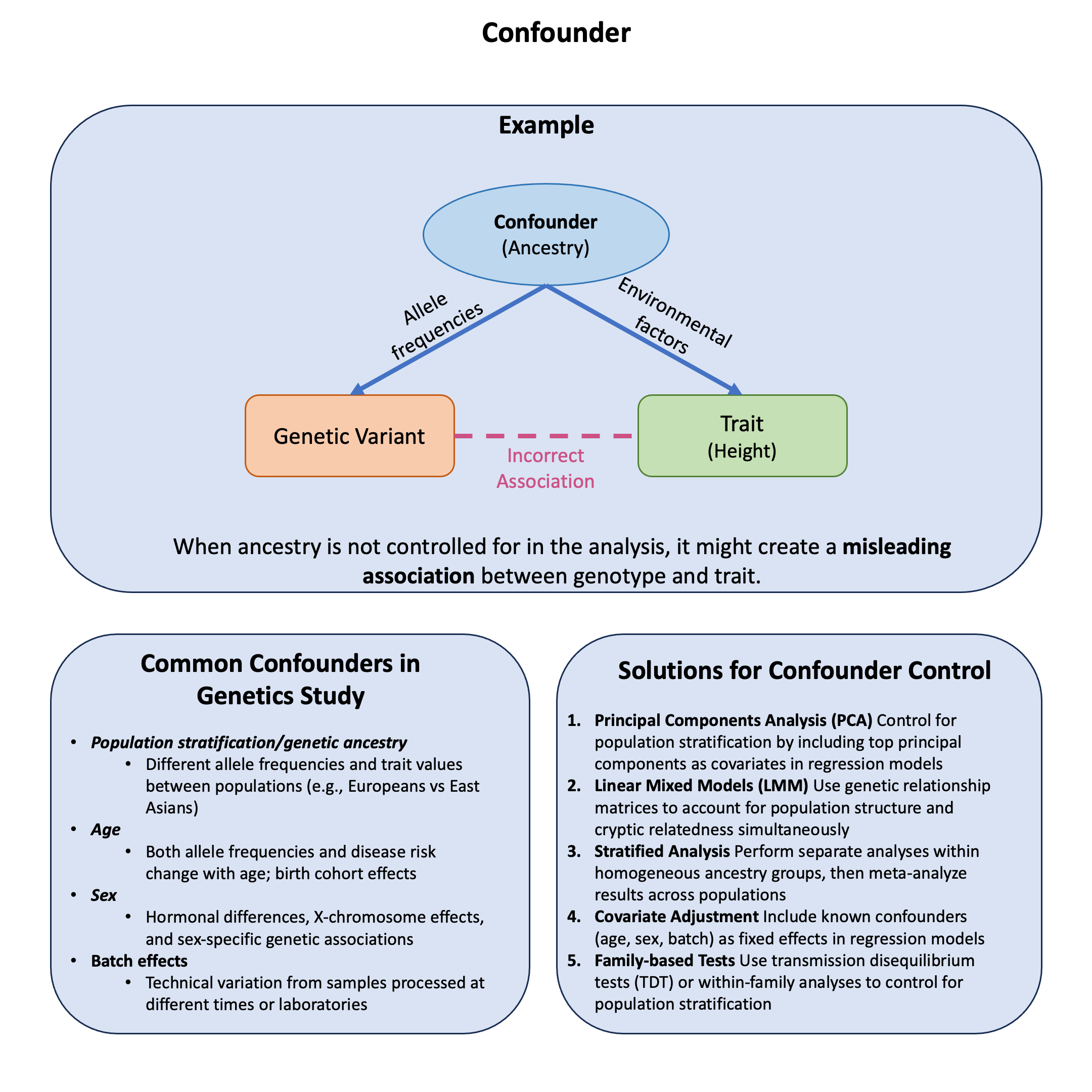
Graphical Summary#

Fig

Key Formula#

The key formula for the concept of a confounder is represented in a causal diagram as:

\[ X \leftarrow W \rightarrow Y \]

Where:

  • \(W\) is the confounder variable

  • \(X\) is the exposure/treatment variable

  • \(Y\) is the outcome variable

  • The arrows \((\leftarrow, \rightarrow)\) indicate the direction of causal influence

This diagram illustrates that a confounder (\(W\)) has a direct causal effect on both the exposure (\(X\)) and the outcome (\(Y\)), creating a “backdoor path” between \(X\) and \(Y\) that must be blocked to obtain an unbiased estimate of the causal effect.

Technical Details#

What Happens When We Ignore Confounders#

When a confounder is present but not controlled:

\[ \text{Observed Association} = \text{True Effect} + \text{Confounding Bias} \]

  • True Effect: The real biological relationship we want to find

  • Confounding Bias: The false association created by the confounder

  • Observed Association: What we actually measure (often misleading!)

The Solution: Control for Confounders#

The most common and practical solution is regression adjustment - simply include confounders as additional variables in your model:

\[ Y = \beta_0 + \beta_1 X + \beta_2 W_1 + \beta_3 W_2 + \ldots + \epsilon \]

Where:

  • \(Y\) = outcome (e.g., height, disease status)

  • \(X\) = genetic variant of interest

  • \(W_1, W_2, \ldots\) = confounders (e.g., age, ancestry, sex)

  • \(\beta_1\) = the unbiased effect of the genetic variant

Here are the common approaches in genetic studies:

  • Principal Components (Most Common): Control for population structure by including top PCs:

    \[ \mathbf{Y} = \mathbf{X}\boldsymbol{\beta} + \text{PC}1 + \text{PC}2 + \text{PC}3 + \text{Age} + \text{Sex} \]

  • Linear Mixed Models: Use genetic relationship matrices for complex population structure:

    \[ \mathbf{Y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{Zu} + \boldsymbol{\epsilon} \]

    where \(\mathbf{u} \sim N(0, \sigma^2 G)\), G is kinship matrix

  • Stratified Analysis: Analyze each ancestry group separately, then combine results:

    1. Europeans: Trait ~ SNP + Age + Sex

    2. Asians: Trait ~ SNP + Age + Sex

    3. Meta-analyze results

The goal is to block backdoor paths while keeping the direct causal path open.

Example#

Recall from our earlier discussion of marginal vs joint effects how a genetic variant can appear protective when analyzed alone but harmful when controlling for other factors. This dramatic reversal illustrates confounding - where ancestry affects both variant frequency and disease risk, creating spurious associations.

The key question: How can ancestry confound genetic associations and lead us to completely misinterpret a variant’s true effect?

rm(list = ls())
set.seed(9)  # For reproducibility

N <- 100  # Sample size

# Create a confounding variable (genetic ancestry)
ancestry <- rbinom(N, 1, 0.5)  # 0 = Population A, 1 = Population B

# Generate genotype that's correlated with ancestry
# Population B has higher frequency of risk allele
variant1 <- ifelse(ancestry == 0, 
                  rbinom(sum(ancestry == 0), 2, 0.2),  # Pop A: low risk allele frequency
                  rbinom(sum(ancestry == 1), 2, 0.8))  # Pop B: high risk allele frequency

# Population B has generally lower disease risk (better healthcare/environment)
# But the variant increases risk within each population
baseline_risk <- ifelse(ancestry == 0, 0.8, 0.1)  # Pop A much higher baseline risk
genetic_effect <- 0.1 * variant1  # Variant increases risk in both populations

disease_prob <- baseline_risk + genetic_effect
disease <- rbinom(N, 1, pmin(disease_prob, 1))  # Ensure prob ≤ 1

# Create data frame
data <- data.frame(
  disease = disease,
  variant1 = variant1,
  ancestry = ancestry
)

As we did previously, ignoring the confounder (in this case, ancestry) will give us an incorrect result:

# Marginal analysis (ignoring ancestry - combining both populations)
marginal_model <- glm(disease ~ variant1, data = data, family = binomial)
marginal_OR <- exp(coef(marginal_model)[2])
marginal_p <- summary(marginal_model)$coefficients[2, 4]

cat("=== MARGINAL EFFECT (combining populations, ignoring ancestry) ===\n")
cat("OR =", round(marginal_OR, 3), ", p =", round(marginal_p, 4), "\n")
cat("Interpretation:", ifelse(marginal_OR > 1, "Harmful", "Protective"), "\n")

=== MARGINAL EFFECT (combining populations, ignoring ancestry) ===
OR = 0.394 , p = 4e-04 
Interpretation: Protective

But if we consider this in the joint model to control for it, we will get the correct answer:

# Joint analysis (controlling for ancestry)
joint_model <- glm(disease ~ variant1 + ancestry, data = data, family = binomial)
joint_OR <- exp(coef(joint_model)[2])
joint_p <- summary(joint_model)$coefficients[2, 4]

cat("=== JOINT EFFECT (controlling for ancestry) ===\n")
cat("OR =", round(joint_OR, 3), ", p =", round(joint_p, 4), "\n")
cat("Interpretation:", ifelse(joint_OR > 1, "Harmful", "Protective"), "\n")

=== JOINT EFFECT (controlling for ancestry) ===
OR = 1.192 , p = 0.6768 
Interpretation: Harmful
Contents